Piecewise Functions
Description/Explanation/Highlights
Video Description of Piecewise Functions
This video explains how to graph and solve piecewise functions.

Piecewise Functions - Steps and Key Points to Remember
To graph or solve a piecewise function, follow these steps:
- The graph below is an example of a piecewise function.
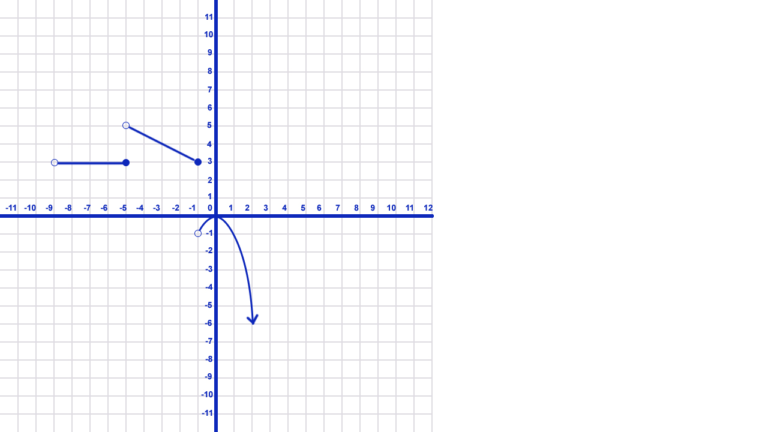
- A piecewise function has different function rules for different intervals on x.
- First, these intervals can’t overlap (or it would no longer be a function). Therefore, -5 is part of the interval from x=-9 to x=-5 in the above example. However, it is not included in the interval from x=-5 to x=-1.
- Secondly, an interval can be infinite. The last interval above starts at x=-1 and goes to infinity, for example.
- Finally, every interval does not have to be defined. Futhermore, intervals can connect but don’t have to. For example, the interval where x is less than or equal to -9 is undefined.
- To write the function defined by the graph, write a function rule for each interval in the function .
- The first (leftmost) interval in the example extends from -9 to -5 including -5 but not -9 (because of the open circle). As a result, write: \(f(x)=3, -9<x\leq-5\) since for all values of x, f(x) is equal to 3 on this segment.
- The next segment extends from -5 (not included) to -1. It is defined as a line with a slope of \(-\frac{1}{2}\) and a y-intercept of 2.5. Therefore, this function rule is: \(f(x)=-\frac{1}{2}x+2.5, -5<x\leq-1\).
- Finally the last segment is an infinite segment. It extends from -1 (not included) to positive infinity. This segment is defined by a parable that has been reflected over the x-axis. Furthermore, it represents the negative quadratic parent function. It is therefore written as: \(f(x)=-x^2, -1<x<\infty\)
Interested in learning to create your own WordPress website or blog in quick, easy lessons?
- Once each interval in the function is defined, write them together as one function. As a result: \(f(x)=\left\{\begin{array} {11} 3, & \quad -9<x\leq-5 \\ -\frac{1}{2}x+2.5, & \quad -5<x\leq-1 \\ -x^2, & \quad -1<x<\infty \end{array} \right. \)
- Moreover, since the last interval goes to positive infinity, write the function as: \(f(x)=\left\{\begin{array} {11} 3, & \quad -9<x\leq-5 \\ -\frac{1}{2}x+2.5, & \quad -5<x\leq-1 \\ -x^2, & \quad x>-1 \end{array} \right. \)
- Now use this function to solve a problem when we know the value of x. For example, when x=2, we know that x falls in the last interval since it is greater than -1. Plug the value of x (2) into \(-x^2\) and solve it. For example, \(-(2)^2=-4\), therefore \(f(x) = -4\) or \(y=-4\).
- If x=-7, f(x)=3 since any value of x in the interval between -9 and -5 (inclusive) is equal to 3.
- x=-2 falls in the middle interval therefore, -2 must be plugged into \(-\frac{1}{2}x+2.5\) to find the value of y or f(x). As a result, plug in -2 to get \(-\frac{1}{2}(-2)+2.5=3.5\) for the value of f(x).
- Any value of x less than or equal to -9 results in an undefined value for f(x). For example, if x is equal to -10, the value for f(x) or y is undefined in this function. Moreover, the domain of this function is restricted to x > -9.
Here are some key points to keep in mind when working with piecewise functions:
- Piecewise functions are recognized by different graph segments on different intervals of x.
- Intervals of x cannot overlap in a piecewise function or it would not be a function.
- There can be infinite intervals, but intervals can connect.
- Some intervals may not be defined therefore, any value of x in these intervals will have an undefined value for y.
- To write a piecewise function from a graph, first write functions for each interval on the graph. Secondly, combine them into one function with the rules for each interval.
- Substitute the value of x into the function rule for the interval where x falls to solve a function for f(x) or y.
Video Highlights of Piecewise Functions
- 00:00 Introduction
- 00:07 Definition of a piecewise function
- 00:28 Example of writing a graph of a piecewise function into function notation
- 04:40 Example of solving for f(x) or y from a piecewise function
- 07:05 Conclusion
To watch this video on YouTube in a new window with clickable highlights, click here

