Interval Notation
Description/Explanation/Highlights
Video Description of Interval Notation
This video explains how to write sets of numbers using interval notation.
Steps and Key Points to Remember When Writing Interval Notation
To write sets of numbers using interval notation, follow these steps:
- Write interval notation using a beginning bracket or parenthesis and an ending bracket or parenthesis.
- Next, write the beginning number of the set followed by a comma and the ending number of the set.
- Brackets indicate that the set includes the beginning and/or ending number.
- For example, write the set of numbers between 3 and 20 as (3, 20).
- To include 3 and 20 in the set, write: [3, 20]. Similarly, to include 3 but not 20, write: [3, 20). Equally important, each of these includes ALL real numbers between 3 and 20.
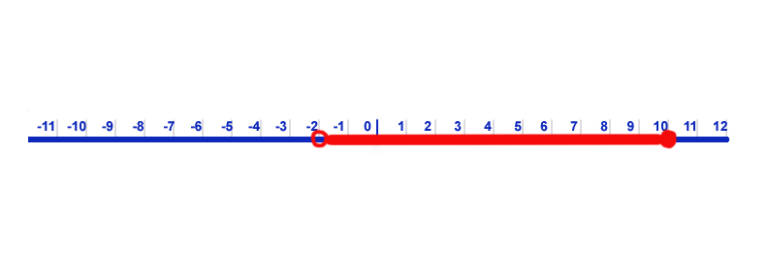
- For example, in the graph above, the red line includes all the numbers between -2 and 10. However, notice that -2 is not included but 10 is included.
- We write this as: (-2, 10]. Use parenthesis at the beginning since -2 is not included. In addition use a bracket at the end since 10 is included.
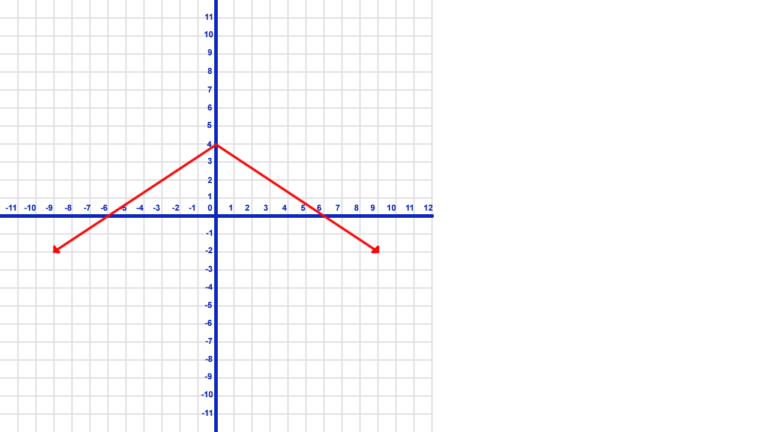
- Using the graph above, first identify the interval on x where \(y>2\). Note that the value of y reaches 2 when x is -3. Furthermore, it continues to be greater than 2 until x reaches 3. Secondly, using those as endpoints, write (-3, 3). Finally, notice the use of parenthesis at both ends since y is equal to 2 but not greater at the endpoints.
- If we change the problem to \(y\geq 2\), write [-3, 3] using brackets indicating that the solutions include -3 and 3.
- Writing the solution for the intervals \(y<2\) is a little more complicated since there are two places on the graph where this is true.
- Notice that y is less than two from negative infinity to -3 and further from 3 to positive infinity. As a result, this creates a union of the two sets of numbers. Write it as: \((-\infty ,-3)\cup(3, \infty )\).
- Write infinity by always using a parenthesis since we never reach infinity. Furthermore, for less than or equal to, use brackets with -3 and 3.
- What if we want to describe the interval where \(y\leq 4\)? That describes all points on the graph therefore, write: \((-\infty , \infty)\).
Interested in learning to create your own WordPress website or blog in quick, easy lessons?
Here are some key points to keep in mind when writing solution sets in interval notation:
- Interval notation is a shorter way to write sets of numbers to describe intervals on lines or graphs. For example, it describes solutions to inequalities or anywhere continuous sets of numbers are used.
- Always start and end with either a parenthesis or a bracket.
- Write the first number in the set by a comma and the last number in the set.
- Brackets indicate that the beginning or ending number is included in the set. Similarly, parenthesis indicate that it is not included.
- There is a bracket on one end and a parenthesis on the other if one number is included and the other is not.
- Negative or positive infinity always uses a parenthesis since we never reach those numbers and the set will never include those numbers.
- Indicate all real numbers by \((-\infty, \infty)\).
Video Highlights
- 00:00 Introduction
- 00:10 Definition and use
- 00:43 Example of how to write all the real numbers between 3 & 20 using interval notation
- 02:08 Describing a set of numbers on a number line using interval notation example
- 03:28 Example of identifying intervals on a graph and writing in interval notation
- 07:30 Summary
- 08:12 Conclusion
To watch this video on YouTube in a new window with clickable highlights, click here
